بهینه‌سازی با استفاده از الگوریتم PSO در MATLAB

دسته‌بندی: برنامه‌نویسی

متلب از پراستفاده‌ترین ابزار در زمینه برنامه‌نویسی علمی بوده و به صورت پیش‌فرض دارای الگوریتم‌های بهینه‌سازی متعددی است. در این مقاله با استفاده از یک مثال ساده به نحوه کار با الگوریتم بهینه‌سازی Particle Swarm Optimization یا PSO در نرم افزار متلب پرداخته می‌شود.

نمایی از نحوه جستجو ذرات برای یافتن پاسخ بهینه در PSO (تصویر از wikipedia)

پیشنهاد می‌شود از سایر مقالات حوزه متلب با استفاده از این لینک دیدن فرمایید. در ضمن حتما برای دریافت آخرین اخبار در حوزه انتشار مقالات جدید در کانال تلگرام این وبسایت به آدرس vdelta_ir عضو شوید.

الگوریتم بهینه‌سازی Particle Swarm Optimization (به اختصار PSO) که در فارسی به "روش بهینه‌سازی ازدحام ذرات" ترجمه شده، یک ابزار قدرتمند و کارآمد برای حل مسائل بهینه‌سازی است. این الگوریتم با الهام از رفتار هماهنگ دسته‌های پرندگان (و حتی ماهی‌ها!) و شیوه تعیین موقعیت آن‌ها با توجه به تجربه شخصی و تجربه گروهی اقدام به پیدا کردن پاسخ بهینه می‌نماید. این الگوریتم توسط جیمز کندی و راسل ابرهارت در سال 1995 توسعه داده شد و به دلیل سادگی و کارایی در حل مسائل پیچیده بهینه‌سازی توجه بالایی را به خود جلب کرده است. در طول سالیان اخیر چندین ویرایش مختلف از این الگوریتم توسعه داده شده و در هر ویرایش عملکرد آن با بهبودهایی همراه بوده است. در این مقاله با استفاده از یک مثال بسیار ساده به پوشش این الگوریتم در متلب پرداخته می‌شود.

یکی از مزایای متلب آن است که به صورت پیش‌فرض یک نسخه استاندارد از الگوریتم PSO در آن پیاده‌سازی شده و در دسترس کاربران قرارگرفته است. این الگوریتم تحت یک تابع با عنوان particleswarm قابل فراخوانی است. الگوریتم PSO متلب به کاربر امکان تغییر تنظیماتی نظیر جمعیت تعداد ذرات (swarm size)، حداکثر تعداد مجاز برای تکرارها (MaxIterations)، استفاده از توابع بهینه‌سازی ترکیبی (HybridFcn) و ... را می‌دهد. یکی از کاربردهای اصلی این الگوریتم یافتن پاسخ‌های نزدیک به حالت بهینه برای مسائل غیرخطی و پیچیده‌ای است که قابلیت حل به صورت خطی با الگوریتم‌های ریاضی (نظیر برنامه‌ریزی خطی) را ندارند. با این الگوریتم صرفا با نوشتن یک تابع در فرمت MATLAB و تعریف کران بالا و پایین متغیرها میتوان اقدام به بهینه نمودن تابع هدف دلخواه نمود.

لازم به ذکر است که PSO متلب به صورت پیشفرض اقدام به حداقل نمودن تابع هدف میکند و برای مسائلی که در آن ها نیاز است تا تابع هدف ماکزیمم شود، میبایست از یک ضریب منفی در تابع هدف استفاده شود. در این صورت حداقل سازی تابع هدف منفی شده عملا منتهی به حداکثر سازی تابع هدف می‌نماید.

در استفاده از PSO باید به این نکته آگاه بود که بر خلاف روشهای ریاضی، PSO یک الگوریتم بهینه‌سازی فراابتکاری بوده که در هر اجرا ممکن است به یک نقطه بهینه متفاوتی برسد. لذا برای رسیدن به پاسخ بهینه واقعی (global optimum) و اجتناب از گیر افتادن در نواحی بهینه محلی (local optimum) نیاز است تا برای یک مسئله خاص اقدام به اجرای چندین باره این الگوریتم نمود تا از بهینگی پاسخ اطمینان نسبی (و نه قطعی) حاصل شود. 

فرمت کلی استفاده از دستور particleswarm به همراه تنظیمات الگوریتم به فرم زیر است:

options = optimoptions("particleswarm", "SwarmSize", 100, "HybridFcn", @fmincon);

[x,fval,exitflag,output,points] = particleswarm(fun,nvars,lb,ub,options);

همانطور که دیده می‌شود در کد بالا از یک دستور برای تعیین تنظیمات و از دستوری دیگر برای اجرای الگوریتم بهینه‌سازی استفاده می‌شود.

*در نسخه‌های قدیمی‌تر متلب یک رابط کاربری گرافیکی برای استفاده از الگوریتم‌های مختلف بهینه‌سازی وجود داشت که در نسخه‌های جدید حذف گردیده است. 

تنظیمات

برای تنظیمات از تابع optimoptions استفاده شده و در این مثال در آن نوع الگوریتم بهینه‌سازی (particleswarm)، تعداد جمعیت ذره‌ها (SwarmSize, 100) و تابع ترکیبی (HybridFcn, @fmincon) تعیین گردیده است. تعداد جمیعت ذره‌ها تعیین کننده تعداد ذراتیست که در هر تکرار از حلقه PSO اقدام به محاسبه تابع هدف شده، تابع ترکیبی یک الگوریتم بهینه‌سازی است که با پایان کار PSO از نتایج این الگوریتم استفاده کرده و در جهت بهتر شدن این نتایج کار بهینه‌سازی را ادامه می‌دهد. لازم به ذکر است که ورودی‌های optimoptions (مربوط به الگوریتم PSO) محدود به این موارد نبوده و می‌‍تواند تنظیمات دیگری را نیز شامل شود. این تنظیمات بسیار مهم بوده و در رابطه با هر یک مطالعات گسترده‌ای انجام شده است. برای نمونه یکی از مطالعاتی که نظر بنده را نیز جلب کرد، مقاله شکل 1 است که در جستجوی Swarm Size بهینه اقدام به اجرای شبیه‌سازی‌های گسترده کرده و به نتایج جالبی می‌رسد. مطالعه این مقاله حتما پیشنهاد می‌شود.

شکل 1- مقاله بررسی اثر Swarm Size

دستور بهینه‌سازی

در دستور اجرای بهینه‌سازی (تابع particleswarm) نیز به ترتیب تابع هدف (fun)، تعداد متغیرها (nvars)، کران پایین متغیرها (lb)، کران بالای متغیرها (ub) و تنظیمات الگوریتم (options که از دستور optimoptions نتیجه شده)، درج می‌گردد. این فرم کلی از یک الگوریتم بهینه سازی PSO بوده که از طریق متلب فراخوانی شده است. تابع هدف الگوریتم PSO (fun) یک تابع است که باید با استفاده از یک function handle (به زبان خودمانی تر استفاده از @ قبل از نام تابع) به الگوریتم PSO داده شود. نگران چیستی @ نباشید، در مثال آتی نحوه استفاده از آن ارائه گردیده است. در این مثال یک ترفند برای انتقال پارامترهای ثابت به تابع هدف بدون استفاده از متغیرهای global نیز آموزش داده می‌شود. 

خروجی های تابع particleswarm نیز x (مقدار بهینه متغیر)، fval (مقدار بهینه تابع هدف)، exitflag (وضعیت خروج از حلقه بهینه سازی)، output (خلاصه ای از وضعیت بهینه سازی) و points (آخرین وضعیت ذرات و مقادیر تابع هدف متناظر با هر یک) هستند.

مثال

برای آن که ساختار یک کد بهینه‌سازی با PSO را ببینیم به یک مثال خواهیم پرداخت. در این مثال قصد داریم تا حداقل میزان تابع هدف شکل 2 را به ازای متغیرهای بین -3 و +3 پیدا کنیم. متغیر x در این تابع، متغیر اصلی تابع بوده و a، b، c و d پارامترهای ثابتی هستند که ضرایب این تابع درجه 3 را تعیین می‌کنند. شاید این سوال پیش بیاید که چه اصراری بر این بود تا تابع به این شکل نوشته شود و پارامترهای ثابت به صورت دستی در تابع تایپ نشده‌اند؟ دلیل اصلی این کار نمایش نحوه انتقال پارامترهای ثابت به الگوریتم بهینه‌سازی PSO با استفاده از عملگر @ است. مقادیر پارامترهای ثابت عبارت است از: a = -1، b = 4، c = 1، d = -1. در شکل 3 مقادیر تابع هدف به ازای مقادیر x بین -3 و +3 ترسیم شده است. 

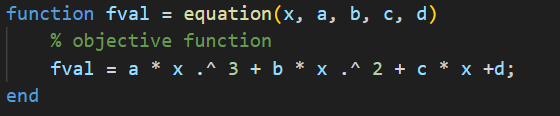
شکل 2- تابع هدف مثال

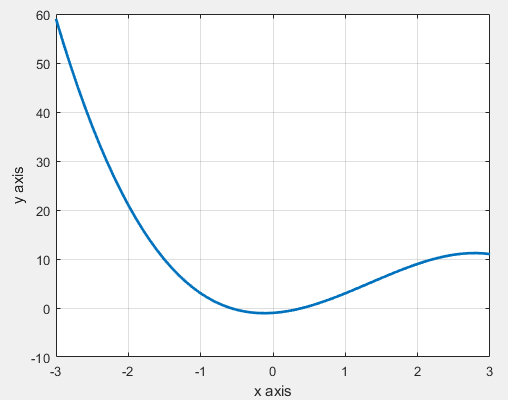
شکل 3- نمایی از تابع هدف مثال

حال قصد داریم تا با استفاده از الگوریتم PSO متلب اقدام به یافتن حداقل مقدار تابع هدف به ازای مقادیر x بین -3 و +3 نماییم. ساختار کلی کد در شکل 4 آورده شده است. تابع هدف مورد استفاده در PSO با نام equation یک متغیر و 4 پارامتر دارد. متغیر و پارامترها همه ورودی این تابع هستند و در این مثال تابع ما 5 ورودی دارد. اما الگوریتم PSO فقط یک متغیر را برای بهینه سازی تغییر میدهد و میبایست برای چهار ورودی دیگر که پارامترهای ثابت تابع هدف هستند، فکری شود.

برای این کار، این تابع و متغیر آن به شکل آنچه در شکل 4 آورده شده در func مقداردهی می‌شود. این دستور تابع equation را در func ذخیره کرده و x را به عنوان متغیر func تعیین می‌کند. به شیوه استفاده از اپراتور @ در این مثال توجه کنید. این شیوه استفاده از @ یعنی func یک ورودی داشته (@(x)) و آن متناظر با متغیر x (اولین ورودی از تابع equation) است. در کنار این پارامترهای a,b,c,d نیز به صورت پارامترهای ثابت مقداردهی شده‌اند (توجه کنید که داخل پرانتز بعد از @ پارامترهای a,b,c,d نوشته نشده اند و در داخل خود آرگومان تابع آورده شده اند.). اگر این کار را نمیکردیم، مجبور به استفاده از یک راهکار غیر بهینه به نام global variables بودیم که خود نیازمند مقاله ای جداگانه اند. اما این بحث در این قسمت از مقاله برای آن دسته از کاربران حرفه‌ای تر متلب نوشته شد که از متغیرهای global برای حل مشکل انتقال پارامترهای ثابت به تابع تحت بهینه‌سازی استفاده می‌کنند.

حال می‌توان func را به عنوان تابع هدف به PSO داده و PSO با تغییر تک متغیر آن (متغیر (x)) اقدام به پیدا کردن نقطه بهینه (نقطه مینیمم) می‌کند. تعداد متغیرهای این تابع 1 عدد بوده (nvars = 1) و کران پایین (lb=-3) و کران بالای آن (ub=3) نیز همانند شکل 4 تعریف شده‌اند. همچنین تعداد Swarm Size نیز برابر با 50 ذره در نظر گرفته شده است که با توجه به مسئله و تعداد متغیر قدری زیاد است. مختصات x و y نقطه بهینه در انتهای شکل 4 آورده شده است. این مختصات با استفاده از دستور disp چاپ شده که شیوه استفاده از آن در تصویر موجود است.

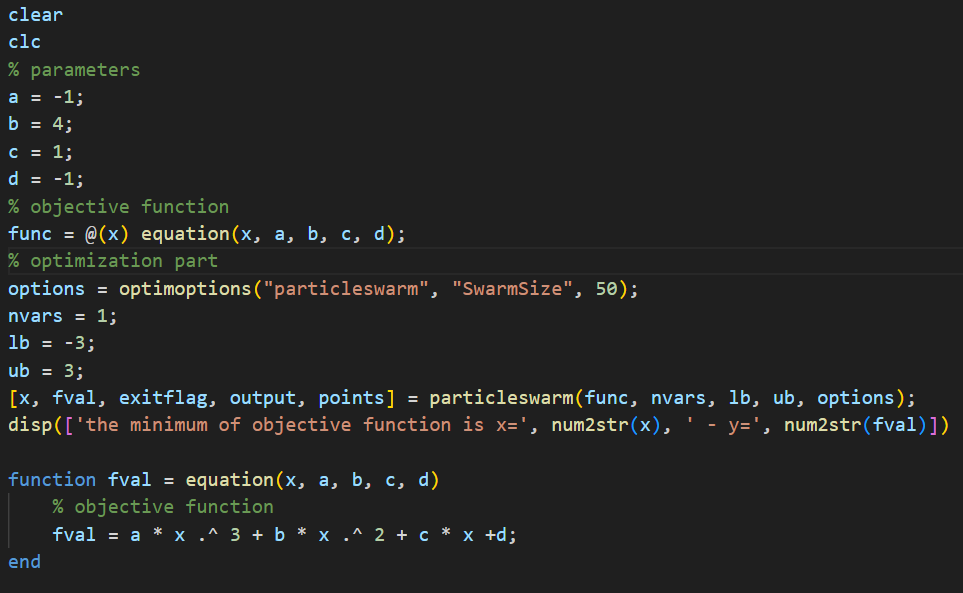
شکل 4- نمای کلی یک مثال ساده برای استفاده از PSO متلب

این مثال بینهایت ساده بوده و در عمل مسائلی که با آن سروکار داریم چندین برابر پیچیده تر هستند. اما نکته جالب این جاست که مستقل از پیچیدگی مسئله روند استفاده از از این الگوریتم تفاوت چندانی نمی‌کند! شاید لازم باشد تا تعداد متغیرها (nvars) و lb,ub تغییر داده شود اما اصل کار همچنان مشابه با این مثال ساده است. 

اگر تعداد متغیرها بیش از 1 عدد باشد، اولا که باید پارامتر nvars به تعداد متغیرها تغییر داده شود. برای مثال در صورتی که مسئله ای با 5 متغیر داشته باشیم:

nvars=5;

پارامترهای مربوط به کران های بالا و پایین نیز در این صورت میبایست بروزرسانی شوند. برای مثال در صورتی که کران پایین همه این متغیرها برابر با -3 و کران بالای آن ها برابر با 3 باشد، پارامترهای lb,ub به این صورت می‌شود:

lb = [-3, -3, -3, -3, -3];

ub = [+3, +3, +3, +3, +3];

یعنی در ماتریس پارامترهای lb,ub می‌بایست به تعداد متغیرها مقدار داشته باشیم. 

این مقاله صرفا برای ایجاد یک آشنایی اولیه با الگوریتم PSO نوشته شد. لذا از تشریح بسیاری از نکات، تنظیمات و پارامترهای این الگوریتم در متلب صرف نظر شد. لذا توصیه میشود برای مطالعه بیشتر در رابطه با الگوریتم به راهنمای متلب مراجعه فرمایید:

لینک راهنما

پایان.