بهینه‌سازی با استفاده از الگوریتم ژنتیک در MATLAB

دسته‌بندی: برنامه‌نویسی

با نگاهی به مقالات سال‌های اخیر می‌توان دید که الگوریتم ژنتیک یکی از مهم‌ترین ابزارهای بهینه‌سازی در دست مهندسان (علی الخصوص مهندسین برق قدرت) بوده است. خبر خوب آنجاست که کاربران متلب برای استفاده از این الگورتیم به یکی از بهترین پیاده‌سازی‌های آن دسترسی دارند. در این مقاله با استفاده از یک مثال به نحوه استفاده از الگوریتم ژنتیک (genetic algorithm) در MATLAB پرداخته خواهد شد.

نمایی از نحوه حرکت به سمت پاسخ بهینه در یک الگوریتم تکاملی نظیر genetic algorithm (تصویر از wikipedia)

الگوریتم ژنتیک (genetic algorithm یا ga) یک الگوریتم فراابتکاری است که در آن با الهام از «انتخاب طبیعی» (زیرشاخه ای از الگورتیم های تکاملی) اقدام به اجرای عملیات بهینه سازی می‌شود. از الگوریتم ژنتیک معمولاً برای تولید راه‌حل‌های با کیفیت بالا برای مسائل بهینه‌سازی و جستجو استفاده می‌شود. در این دست از الگوریتمها عمل بهینه سازی و حرکت به سوی یافتن پاسخ بهینه با استفاده از عملگرهای بیولوژیکی مانند انتخاب (selection)، ترکیب (crossover) و جهش (mutation) انجام می‌شود.

الگوریتم ژنتیک قادر است تا در طیف وسیعی از مسائل مهندسی نسبت به یافتن پاسخ‌های بهینه اقدام نماید. این کاربرد می‌تواند از جنس بهبود عملکرد یک سیستم، جایابی تجهیزات، مسیریابی، مدیریت دارایی‌ها و حتی طراحی ادوات جدید باشد. برای نمونه یکی از مثال‌های جذاب از کاربرد الگوریتم ژنتیک در شکل 1 ارائه گردیده است. این تصویر مربوط به آنتن فضاپیمای NASA ST5 به تاریخ سال 2006 را نشان می‌دهد. این فرم و شکل پیچیده و حتی عجیب آنتن توسط یک الگوریتم طراحی تکاملی (نظیر الگوریتم ژنتیک) ایجاد شده تا بهترین الگوی تابش را ایجاد کند. این آنتن به عنوان یک آنتن تکامل یافته (evolved antenna) شناخته می‌شود. 

شکل 1- تصویر آنتن فضاپیمای NASA ST5 در سال 2006 (تصویر از ویکیپدیا)

با توجه به این که هدف اصلی از این مقاله استفاده از MATLAB برای اجرای بهینه سازی با الگوریتم ژنتیک بوده، ابتدا مقدمه ای کوتاه پیرامون تشریح روش کارکرد این الگوریتم ارائه شده و سپس به بحث برنامه نویسی در متلب پرداخته خواهد شد. 

در الگوریتم ژنتیک جمعی از پاسخ‌های انتخابی (جمعیتی متشکل از پاسخ‌های کاندید شده) در طول مسیر بهینه‌سازی به سمت پاسخ‌های بهتر «تکامل» می‌یابند. هر کاندید مشخصه‌هایی دارد (کروموزوم‌ها) که می‌تواند جهش یافته و تغییر یابد. به طور سنتی پاسخ‌های کاندید شده از جنس دودویی (باینری، binary، یا 0 و 1) بوده ولی اقسام دیگری از روش‌های تعریف هر کاندید وجود دارد. برای نمونه در متلب پاسخ‌های کاندید بسته به تعریف کاربر می‌تواند برای مثال به صورت دودویی و یا double-precision floating point باشد. 

اولین جمعیت از پاسخ‌ها عموما به صورت تصادفی ایجاد شده و در طی مسیر بهینه سازی و هر تکرار (که به هر تکرار در اصطلاح نسل یا generation گفته می‌شود) به سمت پاسخ بهینه حرکت مینماید. در هر تکرار مقدار تابع هدف به ازای هر عضو از جمعیت محاسبه می‌گردد. در جمعیت هر نسل پاسخ‌هایی که تابع هدف بهتری دارند انتخاب شده و بر اساس آن جمعیت نسل‌های جدیدتر پدید می‌آیند.

مثال

فرض کنید تابعی نظیر آنچه در رابطه (1) ارائه گردیده است، داشته باشیم. با فرض آن که x1، x2 و x3 سه متغیر حقیقی باشند، حداقل مقدار y زمانی رخ می‌دهد که 3 جمله تشکیل دهنده رابطه (1) برابر با صفر باشند. هرچند حداقل پاسخ این رابطه با یک نگاه به رابطه آن واضح است و ریشه هر جمله را می‌توان به وضوح تشخیص داد اما این مثال ساده خود می‌تواند یک نقطه شروع خوب برای ورود به بحث برنامه‌نویسی باشد.

(1)	y=(x1-2)2+(x2-3)2+(x3-1)2

متن برای شروع کار بهینه‌سازی ابتدا لازم است تا تابع هدف (رابطه (1)) به صورت یک تابع متلب با نام exampleFunc نوشته شود. کد این تابع در شکل 2 ارائه گردیده است. ورودی این تابع ماتریس x است که می‌بایست 3 درایه داشته باشد. درایه های اول تا سوم این ماتریس متناظر با متغیرهای x1، x2 و x3 در رابطه (1) هستند. 

شکل 2- تابع هدف این مثال در متلب

حال که تابع هدف نوشته شده، می‌توان آن را به عنوان یک تابع برای اجرای بهینه‌سازی به الگوریتم ژنتیک (ga) متلب داد. قبل از این کار ابتدا نگاهی به شیوه استفاده از دستور الگوریتم ژنتیک متلب در شکل 3 داشته باشیم. همانطور که دیده میشود بسته به این که مسئله مورد نظر برای بهینه سازی چه قیودی دارند (قیود نامساوی و تساوی خطی، قیود غیر خطی، کران بالا و پایین برای متغیرها و امثالهم) دستور مورد نیاز برای اجرای شبیه سازی متفاوت است. 

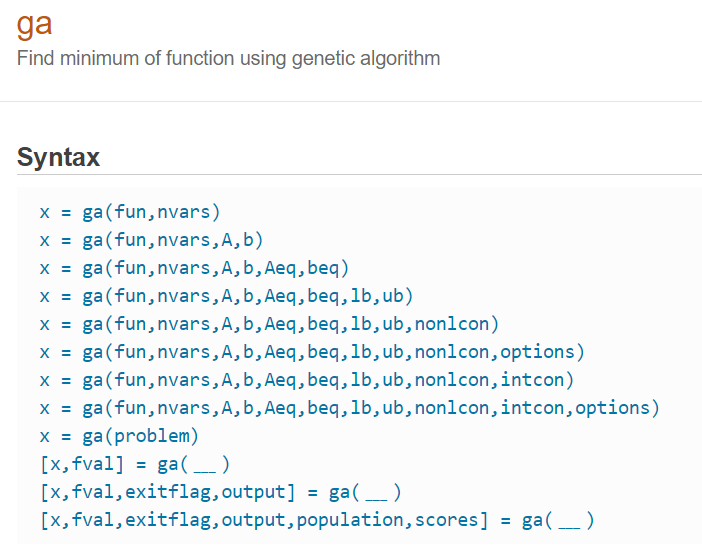
شکل 3- تصویری از مستندات متلب برای دستور الگوریتم ژنتیک

همانطور که در شکل 3 مشخص است دو متغیر fun (تابع هدف) و nvars (تعداد متغیرها) دو ورودی اساسی در این دستور هستند. ورودی fun که اولین ورودی دستور ga محسوب می‌شود، همان تابع هدفیست که برای بهینه‌سازی نوشته شده است. توجه داشته باشید که به صورت پیشفرض، الگوریتم بهینه سازی ژنتیک در متلب در راستای حداقل سازی تابع هدف حرکت میکند. برای آنکه الگوریتم ژنتیک قادر باشد تا از این تابع استفاده کند باید از یک function handler (همان اضافه کردن یک @ ابتدای نام تابع) استفاده شود. برای این کار تابع هدف شکل 2 (exampleFunc) نظیر شکل 4 به objFunc تخصیص می یابد. 

شکل 4- شیوه استفاده از function handler 

برای یافتن حداقل مقدار تابع رابطه (1) به چندین ورودی برای استفاده در دستور ga متلب نیاز داریم. ابتدا میبایست تعداد متغیرها یا nVars را مشخص کنیم که در این مثال برابر با 3 است. پس از این مرحله، نیاز است تا کران بالا و پایین متغیرها را تعیین نماییم. این کار در کد موجود در شکل 5 با استفاده از ماتریس‌های lb (کران پایین یا Lower Bound) و ub (کران بالا یا Upper Bound) انجام شده است. این دو ماتریس مشخص می‌کنند که متغیر الگورتیم ژنتیک در چه بازه‌ای اجازه جستجو دارد. در این مثال این مقدار برای هر سه متغیر از 0 تا 5 در نظر گرفته شده است. توجه داشته باشید که بازه تنظیمی مربوط به lb و ub به شدت به مسئله شما بستگی داشته و میبایست نه آنقدر بزرگ باشد که کار ga را دشوار نموده و نه آنقدر کوچک باشد که پاسخ‌های بهینه احتمالی را در بر نگیرد.

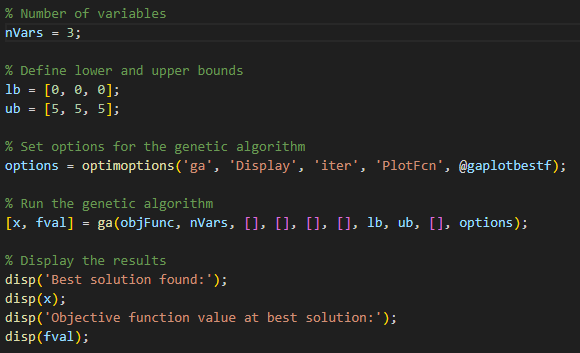
شکل 5- کد نوشته شده برای اجرای الگوریتم ژنتیک

در ادامه نوبت به آپشن‌های استفاده شده (options) و الگوریتم ژنتیک می‌رسد. در دستور optimoptions، پس از مشخص کردن الگوریتم بهینه‌سازی ('ga')، اقدام به تعیین نوع نمایش نتایج در command window با استفاده از دستور 'Display' (تنظیم iter برای Display، نتیجه بهینه سازی در هر نسل از ga را در command window چاپ میکند، این آپشن میتوانست 'off' باشد) و پس از آن تنظیم 'PlotFcn' (تنظیم gaplotbestf برای PlotFcn مشخص میکند که بهترین تابع هدف رسیده شده در هر نسل به چه میزانی بوده است) می‌رسد. در دستور ga نیز هرکجا که از یک قید یا ورودی استفاده نشده، یک ماتریس خالی «[ ]» قرار می‌دهیم. 

هرچند که تنظیمات اولیه موجود در متلب به صورت داینامیک و با توجه به مسئله شما و پارامترهایی نظیر nvars تعیین میگردند، اما به طور کلی آپشن ها در استفاده از الگوریتم ژنتیک بسیار مهم هستند. اگر تنظیمات پیش فرض متلب برای مسئله شما مناسب نبود و پاسخ های مناسبی را از الگوریتم نمی‌گرفتید، همواره امکان تغییر در این تنظیمات نیز وجود دارد. تنظیمات تکمیلی در زیربخش options از input arguments مستندات (documantation) مربوط به ga ارائه گردیده است. برخی از مهم ترین پارامترهای تنظیمی عبارتند از: "InitialPopulationMatrix" مشخص کننده اولین جمعیت شروع بهینه سازی، "PopulationSize" اندازه جمعیت کاندیداهای تحت بهینه سازی در هر نسل، "MaxGenerations" حداکثر تعداد تکرارها (نسلها) پیش از توقف الگوریتم هستند. برای داشتن درکی عمیق تر از عملکرد ga در متلب و در رابطه با تنظیمات تخصصی تر نظیر "CreationFcn"، "CrossoverFcn"، "MutationFcn" و امثالهم به مخاطبان توصیه میشود از مستندات نرم افزار توضیحات هر یک را مطالعه نمایند. 

با اجرای الگوریتم بهینه سازی و به دلیل استفاده از تنظیم "PlotFcn" به مقدار gaplotbestf، در طی اجرای بهینه سازی نموداری به صورت شکل 6 به شکل زنده از وضعیت پاسخها در هر نسل ترسیم می‌گردد. در ادامه و در شکل 7 نیز خروجی نرم افزار با استفاده از 4 خط کد انتهایی شکل 5 ارائه گردیده است.

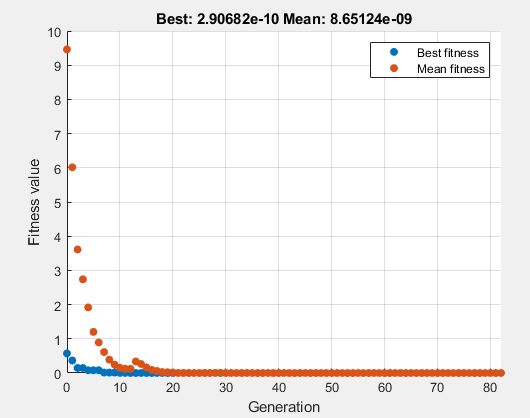
شکل 6 - خروجی ترسیمی الگوریتم ژنتیک از عملکرد خود طی نسل های (تکرارها) مختلف

شکل 7- پاسخ بهینه سازی 

همانطور که دیده میشود، بدون آن که دستورالعمل ریاضی خاصی برای یافتن کمینه رابطه (1) نوشته شود، الگورتیم ژنتیک قادر بود تا صرفا با استفاده از یک الگوریتم تکاملی نسبت به یافتن پاسخ بهینه اقدام نماید. مقادیر 2، 3 و 1 که به عنوان خروجی مشخص شده اند در واقع همان ریشه های معادله (1) بوده و به ازای آن ها مقدار تابع هدف برابر با صفر (کمترین میزان ممکن) میگردد. 

حال اگر تابع هدف ما الگوریتم پیچیده تری داشت چه؟ تنها کاری که در این صورت باید انجام شود این است که تابع هدف جدید خود را بنویسیم و با تغییراتی اندک در دستور نوشته شده برای ga اقدام به اجرای بهینه سازی نماییم. مستقل از تنظیمات بهینه برای مسائل مختلف، الگورتیم ژنتیک نسبت به مسئله ای که قصد بهینه سازی آن را داریم مستقل است. یعنی الگوریتم ژنتیک هم میتواند در یک مسئله مربوط به هماهنگی حفاظتی میان رله های اضافه جریان استفاده شده و هم در مسئله ای مربوط به کاهش هزینه های بهره برداری در یک صنعت خاص. این سطح از استقلال سبب میشود تا این الگورتیم ابزاری مناسب برای یافتن پاسخ های بهینه در مسائل مختلف باشد.