روش مونت کارلو

دسته‌بندی: متلب برنامه‌نویسی متفرقه

در صنایع مختلف همواره مسائل بزرگ و پیچیده ای وجود دارند که مدلسازی رفتار و خروجی های آن ها با استفاده از روش های ریاضیاتی قطعی یا بسیار دشوار و یا حتی غیر ممکن است. در این مقاله به یکی از ابزارهای محاسباتی با نام روش مونت کارلو پرداخته میشود.

اگر بخواهیم به صورت تک خطی تعریفی داشته باشیم، روش مونت کارلو به دسته ای از الگوریتم های کامپیوتری اطلاق میشود که بر نمونه برداری تصادفی برای رسیدن به نتایج عددی استوار هستند. یعنی مفهوم پایه این روش استفاده از تصادفی بودن برای حل مسائلیست که حتی ممکن هست در ذات خود قطعی (deterministic) باشند. این دست از روش ها از جهت استفاده ای که در برخی از مسائل بهینه سازی و مدلسازی احتمالاتی پدیده های فیزیکی دارند، بسیار مهم قلمداد میشوند. برای مثال پدیده ای احتمالاتی را در نظر بگیرید که در ورودی های خود با عدم قطعیت هایی همراه هستند. به دست آوردن خروجی چنین سیستمی با فرض همه حالات ورودی ممکن، چندان منطقی و امکان پذیر نبوده و روش های مونت کارلو با استفاده از ورودی های تصادفی قرار گرفته در گستره ای مشخص (با در نظر گرفتن توزیع احتمالاتی ورودی ها) حل چنین مسئله هایی را ممکن میکنند. اثربخشی روش های منطبق بر مونت کارلو همواره محل بحث بوده و برای نمونه یکی از چالش های ذکر شده شامل بده-بستان بین دقت و هزینه محاسباتی این الگوریتم به همراه مشکلات ناشی از افزایش تعداد متغیرها و ابعاد مسئله می‌شود. 

اما ساختار مسائل مونت کارلو عموما از یک الگو مشخص پیروی می کند. این الگو به صورت زیر است:

1- تعریف گستره ای از وروی های ممکن

2- تولید ورودی‌های تصادفی منطبق بر یک توزیع احتمالاتی مشخص 

3- اجرای محاسبات قطعی (deterministic) با استفاده از داده‌های گام 2 و گرفتن خروجی ها

4- گردآوری نتایج

برای مثال فرض کنید میخواهیم تخمینی از عدد π با استفاده از روش‌های احتمالاتی داشته باشیم. مساحت یک دایره با شعاع 1 و مرکزیت (0 و 0) در مختصات دکارتی را در نظر بگیرید. مساحت این دایره برابر با π(1)² می‌شود. فرض کنید حول این دایره همانند شکل 1، یک مربع به ضلع 2 (و مساحت 4) وجود داشته باشد. در داخل این مربع اقدام به پراکندن نقاطی تصادفی (با توزیع همگن یا uniform) نمایید. برای این کار میتوان از یک کد MATLAB نظیر شکل 1 استفاده کرد. 

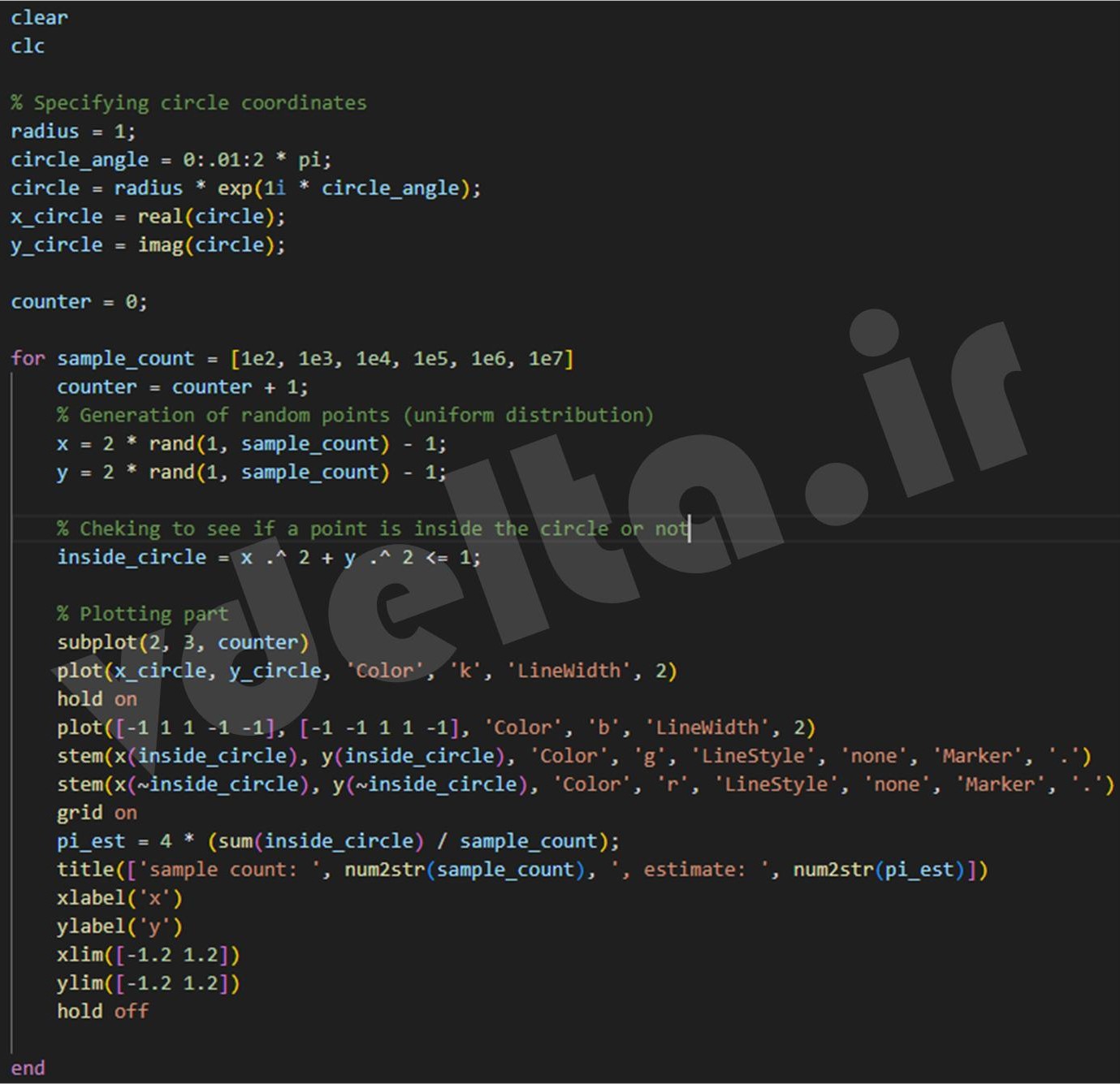
شکل 1- کد استفاده شده برای تخمین عدد پی

در این کد:

• با استفاده از تعداد نمونه های 100 الی 10 میلیون اقدام به پراکندن نقاط تصادفی با توزیعی همگن میشود.
• نقاط تصادفی در گستره بین منفی یک و مثبت یک در هر دو محور افقی و عمودی تعریف میشوند.

بخش ابتدایی از این کد با مقاصد ترسیمی و برای تعریف یک دایره در مختصات دکارتی نوشته شده است. در داخل حلقه for نیز به ازای تعداد نمونه (sample count) مختلف اقدام به تعریف نمونه های تصادفی در راستای محورهای عمودی و افقی (y و x) میشود. سپس با استفاده از یک دستور منطقی، نقاطی که داخل دایره واقع شده اند در متغیر (inside_circle) ذخیره میگردند. حال با یافتن مجموع تعداد نقاط محصور در داخل دایره و تقسیم آن بر تعداد کل نقاط، نسبت مساحت دایره به مربع تخمین زده شده و با ضرب این عدد در 4 (مساحت مربع) عدد پی تخمین زده میشود.

در این شبیه‌سازی دامنه ورودی‌ها در واقع همان مربعی است که حول دایره واقع شده است. در این مثال خاص دو ملاحظه مهم را نباید فراموش کرد:

1- اگر نقاط با توزیع uniform پراکنده نشوند، تخمینی ضعیف حاصل می‌شود. چرا که حل صحیح این مسئله منوط به آن است که هر نقطه از گستره ورودیها شانسی یکسان برای انتخاب شدن داشته باشند. بحث تعریف صحیح توزیع احتمالاتی ورودی ها اثر مستقیم بر کیفیت خروجی ها دارد. برای نمونه اگر در فرایند تولید نقاط تصادفی، نقاطی که به مرکز (0 و 0) نزدیک ترند شانس بیشتری برای انتخاب شدن داشته باشند، این امر سبب میشود که به اشتباه، عدد پی بزرگتر تخمین زده شود. 

2- با بیشتر شدن تعداد نمونه ها دقت محاسبات بیشتر می‌شود. 

در شکل 2 نموداری از تعداد نمونه مختلف و عدد پی تخمین زده شده به ازای هر کدام ارائه گردیده است. این مقادیر بالای هر نمودار درج گردیده است. 

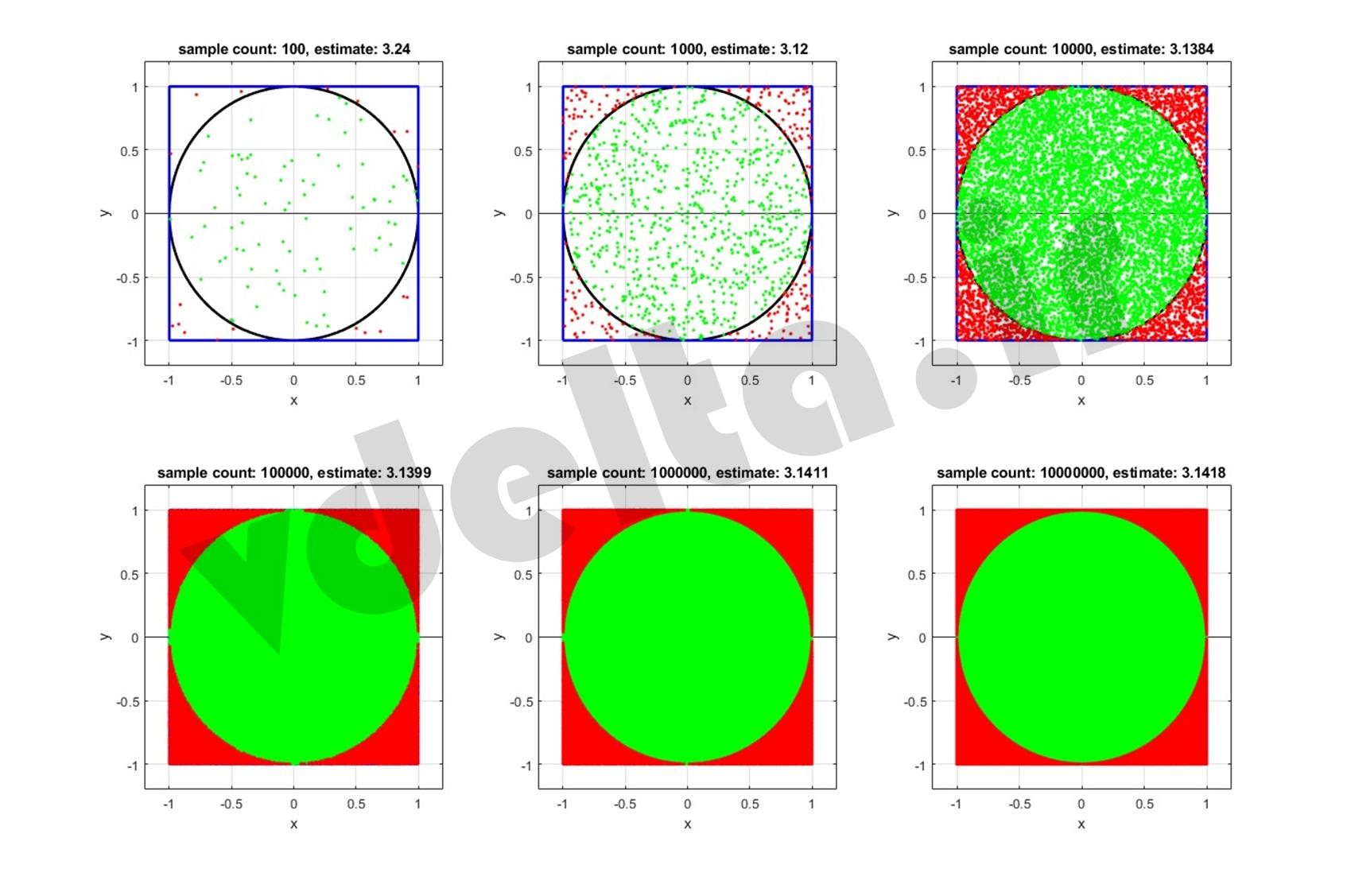
شکل 2- مقدار تخمین زده شده برای عدد پی در ازای تعداد نمونه‌های مختلف

عدد پی برابر با 3.1415926535 بوده و دیده می‌شود که در تخمین‌های موجود در شکل 2 در هنگامی که بیشترین تعداد نمونه انتخاب شده، توانسته با خطایی برابر با 0.0066% این مقدار را تعیین کند. 

مثال ساده ذکر شده در این بخش تنها با هدف نمایش شیوه به کارگیری یک روش احتمالاتی برای به دست آوردن خروجی از مسئله‌ای که در ذات خود چندان احتمالاتی نیست عنوان شده و مفاهیم بنیادین مربوطه را پوشش نمیدهد. در بین تحقیقات و جستجوهایی که داشتم کتاب Essentials of Monte Carlo Simulation: Statistical Methods for Building Simulation Models (شکل 3) یکی از جمع و جور ترین منابع برای شروع به یادگیری این روش است. لازم به ذکر است که کتاب مفصل تری نظیر Simulation and Monte Carlo Method از انتشارات Wiley نیز میتواند برای محققین مفید باشد. 

شکل 3- کتابی مختصر و مفید حول بحث روش مونت کارلو از انتشارات Springer 

مقاله در دست تکمیل ...